【mathematica数学软件】mathematica数学软件下载 v13.1.0 中文免费版
时间:2024/12/23作者:未知来源:三度网教程人气:
软件介绍
mathematica数学软件由Wolfram公司出品的专业数据运算软件,软件涵盖了所有技术计算领域,如神经网络,机器学习,图像处理,几何,数据科学等等,所有功能集中于软件系统当中,能够帮助用户给予高效协同工作,同时软件提供了高效强大的计算方案,它能够处理大规模的并行性,GPU计算量,最大程度为用户带来更高效的工作解决方案。
mathematica中文版软件为全球技术创新人员、教育工作者、学生和其他人士提供了最主要的计算环境,提供集成扩展的系统应用,用户可通过网页浏览器实现云端的远程访问,以及在所有系统上的本地访问。
mathematica数学软件新增内容
一个广泛的系统:Mathematica拥有近5,000个内置功能,涵盖了所有技术计算领域 – 所有这些功能都经过精心集成,因此它们可以完美地协同工作,并且全部集成在Mathematica系统中。
多领域 :基于三十年的发展,Mathematica擅长技术计算的所有领域 – 包括神经网络,机器学习,图像处理,几何,数据科学,可视化等等。
强大的算法能力:Mathematica在所有领域都构建了前所未有的强大算法 – 其中许多都是使用独特的开发方法和Wolfram语言的独特功能在Wolfram创建的。
高水平:超级功能,元算法…… Mathematica提供了一个逐步更高级别的环境,其中尽可能自动化 – 因此您可以尽可能高效地工作。
功能强大:Mathematica旨在提供具有工业强度的功能 – 在所有领域提供强大,高效的算法,能够处理大规模问题,并行性,GPU计算等。
强大的易用性:Mathematica利用其算法能力 – 以及Wolfram语言的精心设计 – 创建一个独特易用的系统,具有预测性建议,自然语言输入等。
文件和代码:Mathematica使用Wolfram笔记本界面,它允许您组织在富文档中执行的所有操作,包括文本,可运行代码,动态图形,用户界面等。
易于学习:凭借其直观的英语功能名称和连贯的设计,Wolfram语言易于阅读,书写和学习。
让你的结果看起来最好:凭借先进的计算美学和屡获殊荣的设计,Mathematica精美地呈现您的结果 – 即时创建顶级的交互式可视化和出版品质的文档。
150,000多个例子:通过文档中心的150,000多个示例,Wolfram演示项目中的10,000多个开放代码演示以及许多其他资源,开始使用几乎所有项目。
即时真实世界数据:Mathematica可以访问庞大的W??olfram知识库,其中包括数千个域中的最新实际数据。
无缝云集成:Mathematica现在可与云实现无缝集成,从而在独特而强大的混合云/桌面环境中实现共享,云计算等功能
连接到一切:Mathematica可以连接到一切:文件格式(180+),其他语言,Wolfram Data Drop,API,数据库,程序,物联网,设备 – 甚至是自身的分布式实例。

mathematica数学软件使用教程
一、【基础运算操作】
1、运算符:Mathematica支持我们常见的运算符+ - * / ^ ! (加,减,乘,除,指数,阶乘)。逻辑运算符&&与,||或,!非
2、表达式:在Mathematica中可以直接将字母符号带入运算,这在大部分的数学软件中是不允许的,如x+y+y=x+2y(字母符号的运算)f=2x(定义一个含有字母的表达式)。
3、书写操作:主要有两点①回车表示换行,Shift键与回车同时按下表示执行程序。②一个表达式以分号;结尾则不输出结算结果,一行可以写多个表达式,但是需要用分号分隔。
4、百分号的用处:%表示上一次的计算结果。
5、内建函数:Mathematica有很多强悍的内建函数,通常以大写字母开头,如常见的Sin[]正弦函数,Plot[]用于函数绘制,Expand[]用于多项式展开等。(注意Mathematica是区分大小写的,所以在写函数时一定注意开头大写,另外紧跟中括号,不要写成小括号。认识并使用常见的内建函数是用好Mathematic的重要途径,在后面会有更加详细的介绍)
第一节基本知识的举例如下:

二、【常量和变量】
1、常量:在Mathematica中常量有整数,有理数,实数,复数和内置常数,特别要说的在附属中,虚数单位用I(大写的i)表示。内置的常数有Pi(圆周率),E(自然对数),Infinity(无限大)等组成。
①、常数的转换:这里常数的转换指的是将数字转化为有理数或者实数,这里就要用到两个内建函数啦(还记得内建函数的知识吗?见1.5)N[x,n]可以将x转化为实数,精度位数为n其中n可以省略,Rationalize[x,dx]将x转化为有理数,误差小于dx
②、数的输出:NumberForm[x,n]将x以n位精度的实数输出,ScientificForm[x]将x以科学计数法的形式输出
2、变量:变量名是字母和数字的组合,其中不能以数字开头,a12是合法的变量名,12a是不合法的变量名(在说变量名能不能用的时候,通常会用“合法”,“不合法”来表示,合法即这个名称可以作为变量名,反之则不行)。在有乘法存在的时候有些人会把乘法和函数名弄错,如x=2;y=3;之后很多人会将xy理解成乘积,实际x*y才是乘积,xy只是一个新的你没赋值过的变量。
①、变量的赋值:变量赋值用等号=来实现,绝大多数编程语言都是,批量赋值可以用大括号加等号{x,y}={1,2}这样x,y就分别等于1或者2了。当你不使用变量是可以给变量一个空值用x=.来实现
②、变量的替换:使用/.和->箭头可以用来替换表达式中变量的数值(还记得什么是表达式么?看看1.2)执行(还记得怎么执行一个语句吗?看看1.3①)f=2x只可以得到f=2x,再执行f/.x->2就可以得到4,也就是将式子中的x用2替换。多变量的时候用f/.{x->1,y->2}来用值替换变量。
③、变量的删除:Clear[]可以用于删除一个变量,在Mathematic里面变量一旦定义就固定了,所以如果多次使用f这个字母可能出现问题,那么我们要定义新的f的时候就需要用Clear[f]将其删除后再重新定义,这点很重要,尤其是在程序变量很多的时候

三、【函数,表和逻辑表达式】
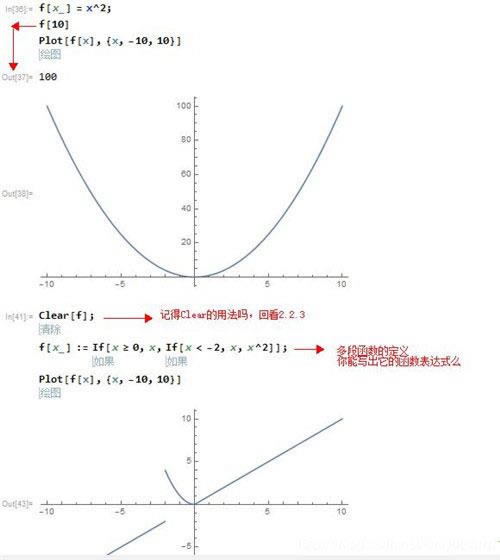
1、函数分为自定义函数和内建函数,这里再列举几个常见的内建函数,如Log[],Round[]四舍五入,Max[]取最大值,Exp[]指数函数,Cos[]余弦。自定义函数的用法是f[x_]=表达式,如表达式可以是x^2,这里的自变量用x_表示,如果是多变量的函数就用f[x_,y_,z_]来表示。除了用等号来定义以外还可以用f[x_]:=表达式,即冒号加等号来定义函数叫做延迟定义,延迟定义的意思是你现在写的只是一个式子,程序并不执行,等到你第一次调用该函数的时候系统才会真正定义(如果你看不懂延迟定义的话不要紧因为不重要,你只要知道冒号等号:=的含义和等号=都是可以定义函数的就可以了)。
①、分段函数的定义:分段函数定义需要使用内建函数If[],如x大于等于0时函数值等于x,函数值小于x时等于x^2,那么我们就应该这样书写该函数f[x_]=If[x>=0,x=x,x=x ^2]。也可以用If实现多段函数的定义。
②、函数调用,调用函数时,不需要像2.2.2那样用替换实现,只需要用f[1]就可以给自变量x赋值了
③、函数的显示:为了直观的展示函数的样子我们用Plot[]绘图功能对函数的样子进行展示,首先我们要定义一个函数或者是一个表达式,用法是Plot[f[x],{x,min,max}]即展示函数f,自变量为x,x的最小值为min最大值为max。(Plot还有很多高级的用法,比如为坐标轴加标注等等,可以绘制出很多漂亮的图形以及三维的图形,这里不详细描述,有需要可以寻找其他资料详细了解)。
2、表:将一些相互关联的元素放在一起就是表,这并不是一个新的概念,2.2.1函数的赋值中{x,y}这样的用法就是一个表,或者叫一个向量,也可以将表达式写成一个表{x,x2,x3}针对表也有很多的操作,这里有个概念就可以了。
3、逻辑表达式:除了数字之外,还有一部分变量用来刻画逻辑,如判断两个变量是否相等的时候用 == 两个等号进行判别,注意不要和赋值运算混淆。常见的有x==y如果x和y相等则返回True,如果不相等则返回False,还有x!=y不等于,x>y大于,x>=y大于等于等等
四、【方程】
前面说了很多Mathematica的基础用法,有人会说这些用法大部分的编程语言都能见到,那么接下来我们就通过方程来展示下Mathematica的优越。
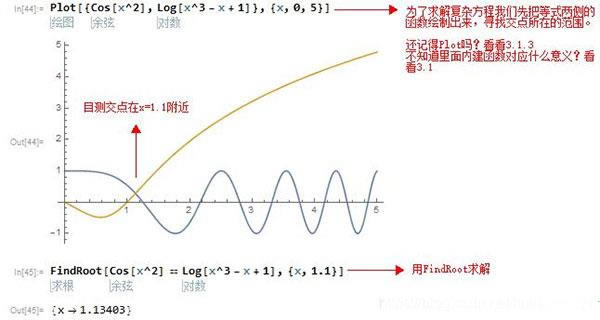
1、方程的表示:以上我们讲到了= 赋值和 = = 判断相等这两个符号(看看3.3)因为等号是赋值的,而我们通常将方程看为一个恒等式,其意义和赋值有一定的区别,所以我们这里用 == 来表示方程的恒等关系,如定义方程:x^2+2x+1==0
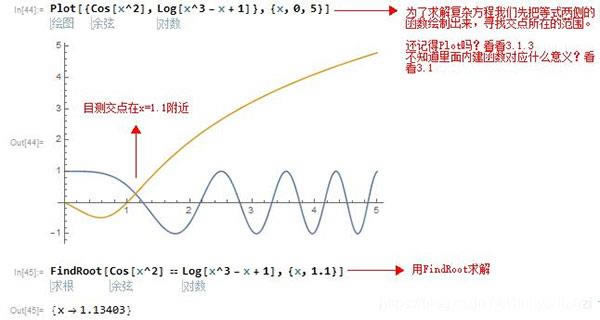
2、方程的求解:解方程需要用到Mathematica的几个内建函数,Slove[等式,{x}],Roots[等式,{x}],FindRoot[等式,{x,x0}],Mathematica总能对不高于4次的函数精确求解,其中Solve和Root用法相同,FindRoot针对解十分困难的方程时,我们通过图像大致知道解的范围,那么我们指定x0,程序会寻找在x0附近的一个解。
3、解方程组,我们也可以用Solve解方程组的根,如Solve[{x+y= =0,x+2y= =6},{x,y}]
4、求方程组的通解,在有变量表达式的方程求解时,Solve[]只能给出部分的解,为了得到各种情况的解我们用Reduce[]来实现,这段话可能说的比较模糊,我们看下面的例子:

五、【微积分的常见操作】
.1、求极限:极限Limit[表达式,x->x0]表示当x趋近于x0时表达式的极限,如何求x趋近于无限大时的极限呢?看看2.1。
2、求微分:微分使用内建函数D[]实现,求f关于x的微分用D[f,x]表示,求f关于x的n阶微分用D[f,{x,n}]表示,求f关于x1,x2的双重偏微分用D[f,x1,x2]表示(D[]的功能非常强大,你可以尝试用此实现链式法则求导)当f函数为单变量的时候求微分也就变成了求导数,用Dt[]函数,其效果和D[]一致
3、求积分:积分使用函数Integerate[]实现,用法为Integrate[f,x]或者Integrate[f,{x,min,max}]前者计算函数f的不定积分,后者给出积分的上下限,计算函数的定积分。注意不是所有的函数都可以计算出不定积分或者定积分,也正因如此引出了数值积分的概念,数值积分使用指令NIntegrate[f,{x,min,max}]用数值计算的方法求得积分的近似值(这里开头的两个字母NI都是大写)。如果说积分函数在给出的下限和上限之间有不连续的点,那么我们需要将点补全

六、【微分方程的求解】
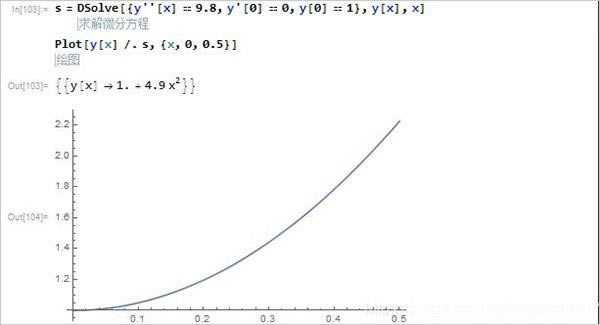
1、微分方程求解:微分方程的求解使用Dsolve[]来完成,其中导数使用跑撇号’表示,n阶导数用n个’表示,如求解y关于x的微分方程DSolve[{微分方程},y[x],x]。求解微分方程组的时候使用DSolve[{微分方程1,微分方程2},{y[x],z[x]},x],求解带有初始条件的微分方程组DSolve[{微分方程,初始条件1,初始条件2},y[x],x]。
2、微分方程的数值解:与积分一样有的微分方程没法给出准确解,所以使用数值方法逼近,NDSolvep[{微分方程,初始条件},y,{x,min,max}]用这个方法可以求得微分方程的数值解,方法类似。
3、微分方程结果的展示:为了绘制微分方程我们需要用一个变量不如s表示问分方程的解,如:x关于y的微分方程s=DSolve[… …],之后使用Plot[y[x]/.s,{x,min,max}]
mathematica数学软件系统要求
跨平台的计算能力,Mathematica 按最新的操作系统和硬件进行优化,从而使您可以在任何系统中使用。
硬件配置
1、处理器:Intel Pentium Dual-Core 或相等的配置
2、硬盘空间:19GB
3、系统内存(RAM):推荐 4GB 以上
4、互联网访问:使用 Wolfram Knowledgebase 在线数据源的必要条件。
Mathematica常用数学函数
Sin[x],Cos[x],Tan[x],Cot[x],Sec[x],Csc[x] 三角函数,其引数的单位为弧度
Sinh[x],Cosh[x],Tanh[x],… 双曲函数
ArcSin[x],ArcCos[x],ArcTan[x] 反三角函数
ArcCot[x],ArcSec[x],ArcCsc[x]
ArcSinh[x],ArcCosh[x],ArcTanh[x],… 反双曲函数
Sqrt[x] 根号
Exp[x] 指数
Log[x] 自然对数
Log[a,x] 以a为底的对数
Abs[x] 绝对值
Round[x] 最接近x的整数
下载地址
- PC版